LSTM原理

结构图

结构图

公式（三道门）

LSTM设计初衷：

下图是RNN的抽象结构单元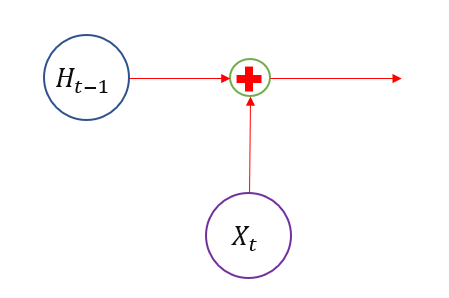
RNN

与传统RNN相比 ，LSTM 增加了三道门，分别用来控制信息的输出量。

  • 对于历史状态: $[{H_{t - 1}}]$ 加一道门，用来控制历史状态信息量，决定丢弃多少信息，${\sigma =1}$ 表示全部保留，${\sigma}=0$表示全部遗忘，我们称为遗忘门。
  • 对于输入信息$X_{t-1}$,我们也希望有一道门来控制其输入量，我们称为输入门 ，输入门决定历史状态的更新。
  • 对于$t$时刻的输出信息，我们也希望有一道门来控制其输出大小，我们称为输出门。

于是就有了，下图是LSTM的抽象结构单元,有$\sigma$的地方就是一个门,
$\sigma$取值0~1.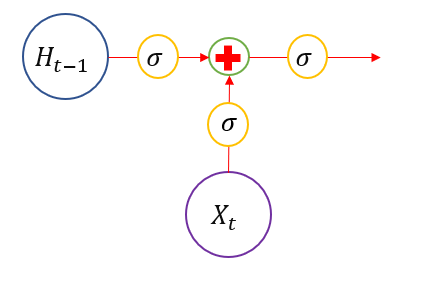
lstm

遗忘门

遗忘门，决定哪些东西被遗忘
$f$ 就是forget的意思。
遗忘门

输入门

输入门 ，决定状态$C_t$的更新
$i$就是input的意思。
输入门
$C_t$​状态更新，与遗忘门和输入门有关
$\tilde{C}{t}$ 不会完全参与到$C_t$的更新中，因为有输入门控制。
${C}{t-1}$ 也不会完全参与到$C_t$的更新中，因为有遗忘门控制。
状态更新

输出门

输出门，决定$t$时刻的输出：
其中，$h_{t-1}$ 为为上个时间节点$t-1$时刻的输出，输出的维度可以设定.
例如pytorch中:

1
rnn = nn.LSTM(10, 20, 2) #(input_size,hidden_size,num_layers)

hidden_size的维度，其实就是设定的hhh的维度，并且每一个时间节点t，都会有一个输出.
输出门
下图给出了对于每个门的输入和输出。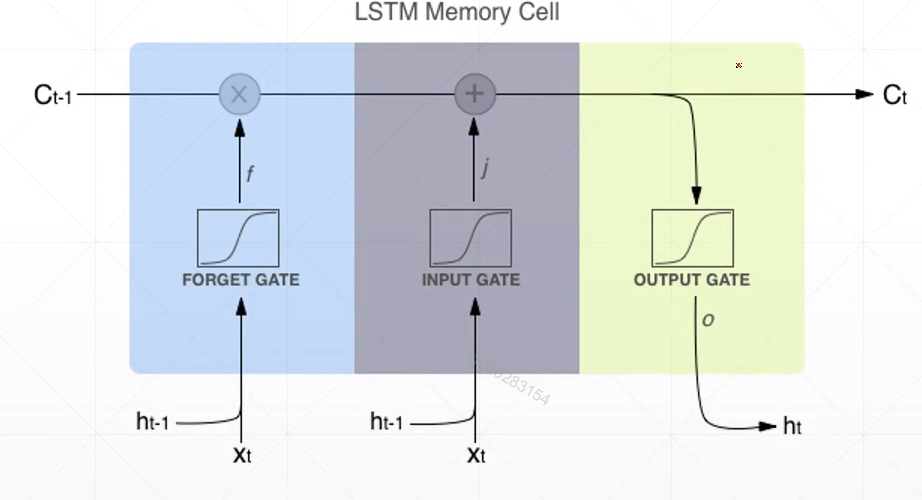
lstm flow
下图说明了每个门的作用。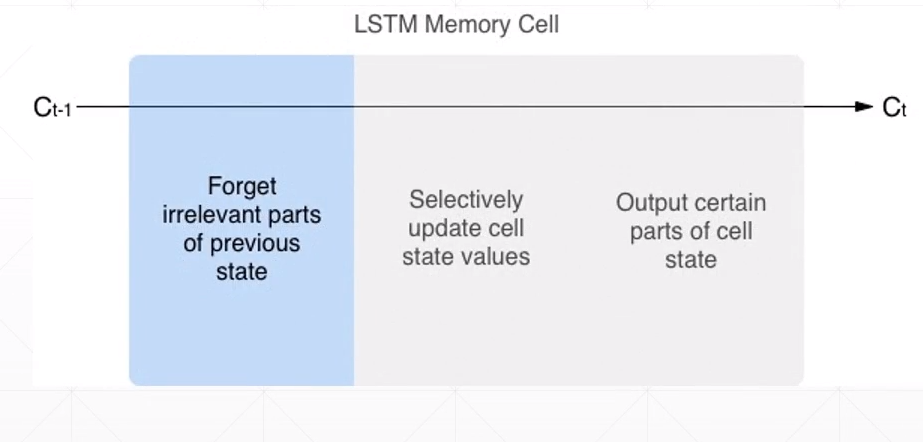
enter image description here

  • $h_{t}$ and $C_t$关系

    $${h_t} = {o_t} \cdot \tanh \left( \right)$$

$h_t$经过了三道门，$C_t$是经过了两道门。