BatchNormal@CV

BatchNorm

批量归一化（batch normalization）层，它能让较深的神经网络的训练变得更加容易，

为什么使用BatchNorm?

• 数据归一化到一定范围（特征缩放-Feature scaling），避免梯度离散，加速收敛。

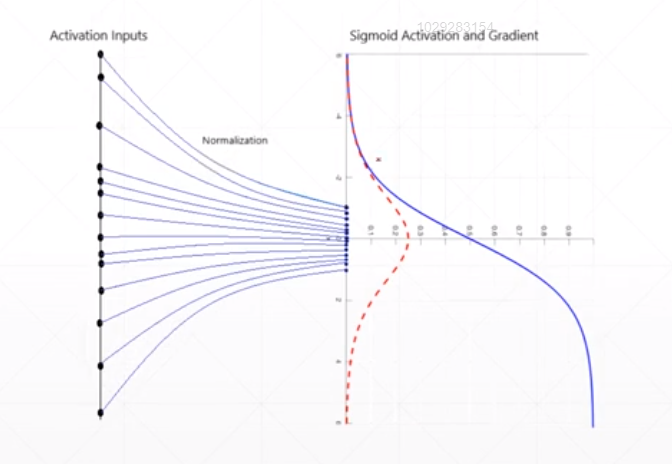
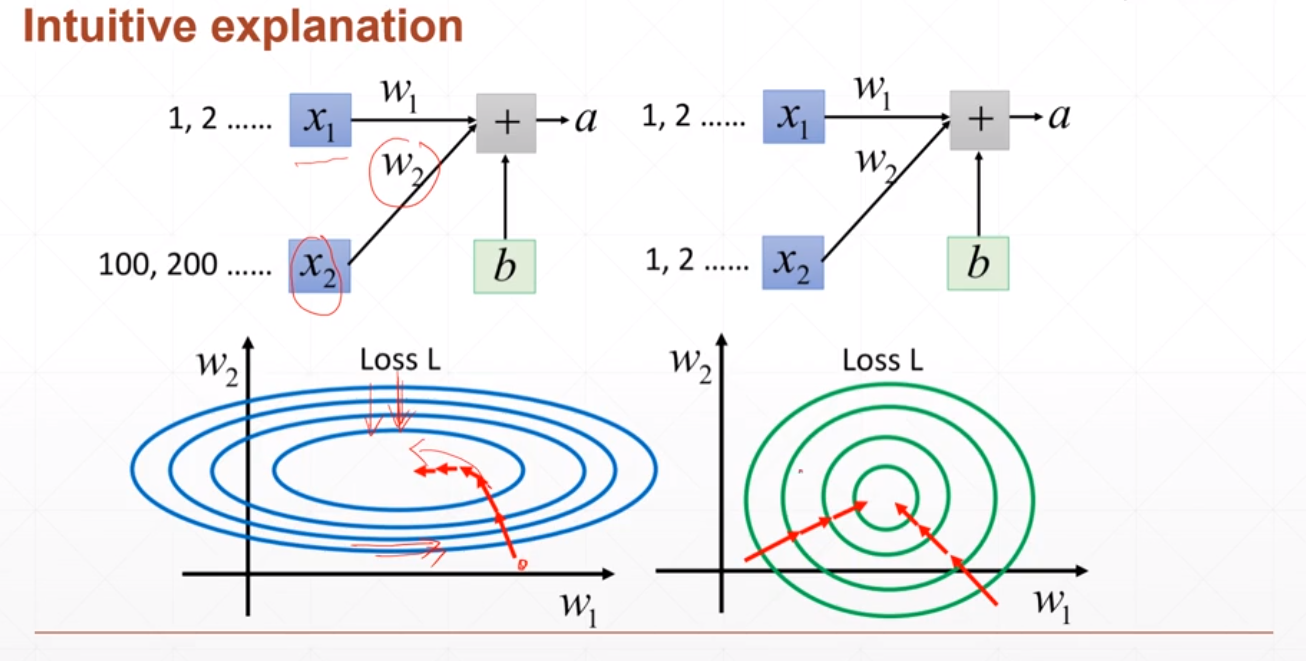
BatchNorm 通常应用在全连接层或者卷积层之后，激活函数之前。如下图所示：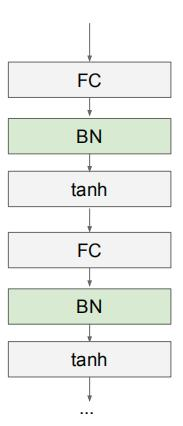

常见BN

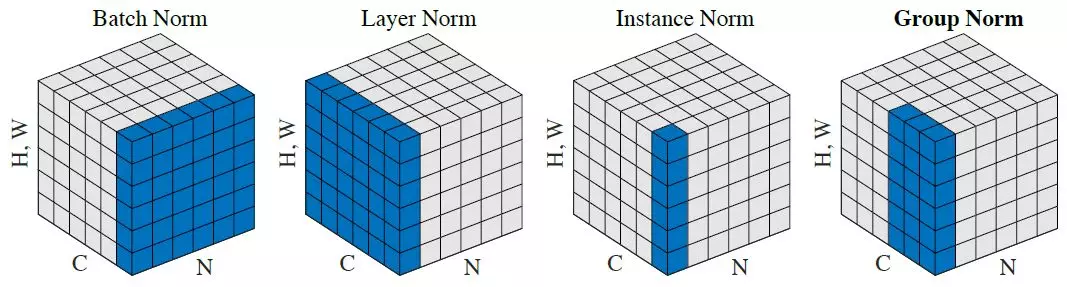
如上图BatchNorm所示:
有N张图片，C个通道，图像大小为$[H,W]$，把图片的维度拍平成$[H \times W]$，
可以得到[N,C,H \times W]的数据格式，取所有图片，分别在每个通道上进行归一化处理，则可以得到$C$（和输入的通道数一致）个归一化结果（均值和方差）。

如上图LayerNorm所示:
取所有每张图片的所有通道数，分别在每张图片上进行归一化处理，则可以得到$N$（和输入的batch大小一致）个归一化结果（均值和方差）。

如上图InstanceNorm所示:
取所有每张图片的每个通道，分别在每张图片每个通道上进行归一化处理，则可以得到$[N,C]$（和输入的batch大小、通道数相关）个归一化结果（均值和方差）。

全连接BN示例

对全连接层做批量归一化

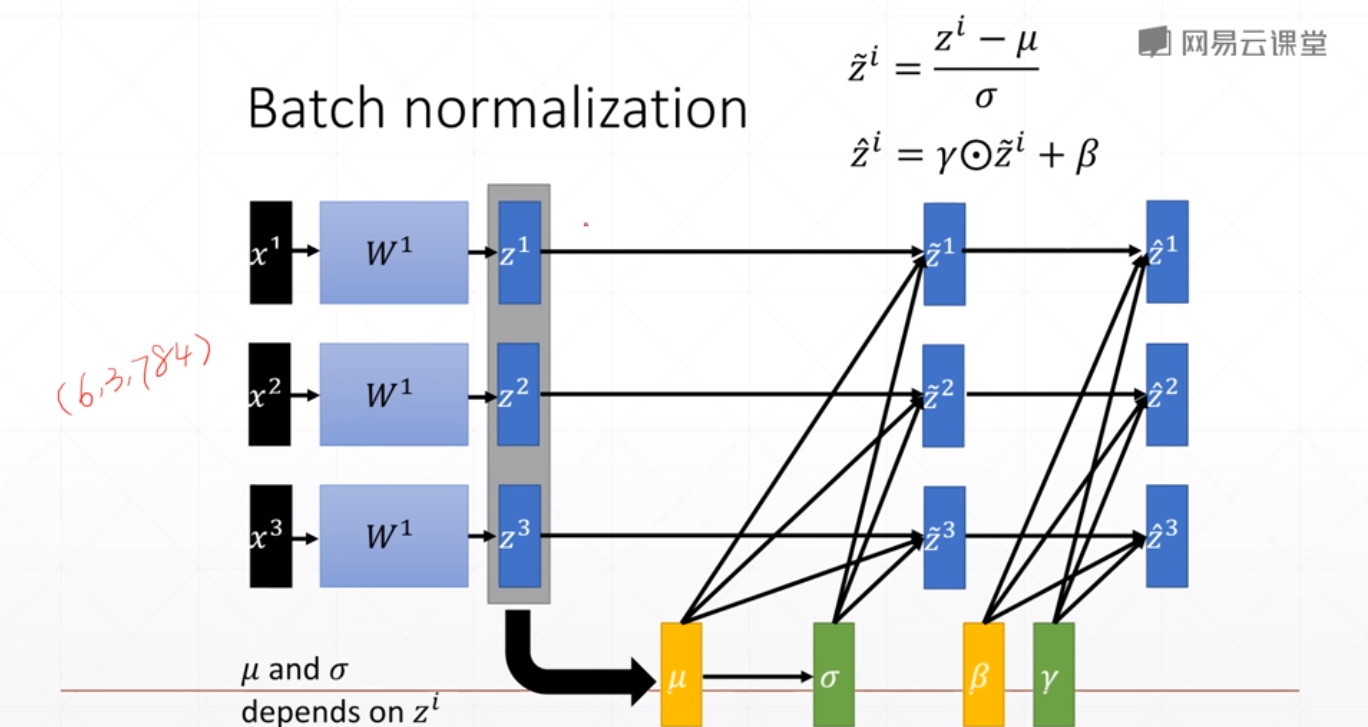
我们先考虑如何对全连接层做批量归一化。通常，我们将批量归一化层置于全连接层中的仿射变换和激活函数之间。设全连接层的输入为$\boldsymbol{u}$，权重参数和偏差参数分别为$\boldsymbol{W}$和$\boldsymbol{b}$，激活函数为$\phi$。设批量归一化的运算符为$\text{BN}$。那么，使用批量归一化的全连接层的输出为

$$\phi(\text{BN}(\boldsymbol{x})),$$
其中批量归一化输入$\boldsymbol{x}$由仿射变换

$$\boldsymbol{x} = \boldsymbol{W\boldsymbol{u} + \boldsymbol{b}}$$

得到。考虑一个由$m$个样本组成的小批量，仿射变换的输出为一个新的小批量$\mathcal{B} = {\boldsymbol{x}^{(1)}$, $\ldots, \boldsymbol{x}^{(m)} }$。它们正是批量归一化层的输入。对于小批量$\mathcal{B}$中任意样本$\boldsymbol{x}^{(i)} \in \mathbb{R}^d, 1 \leq i \leq m$，批量归一化层的输出同样是$d$维向量

$$\boldsymbol{y}^{(i)} = \text{BN}(\boldsymbol{x}^{(i)}),$$

并由以下几步求得。首先，对小批量$\mathcal{B}$求均值和方差：

$$\boldsymbol{\mu}\mathcal{B} \leftarrow \frac{1}{m}\sum{i = 1}^{m} \boldsymbol{x}^{(i)}$$,

$$\boldsymbol{\sigma}\mathcal{B}^2 \leftarrow \frac{1}{m} \sum{i=1}^{m}(\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B})^2,$$
其中的平方计算是按元素求平方。接下来，使用按元素开方和按元素除法对$\boldsymbol{x}^{(i)}$标准化：

$$\hat{\boldsymbol{x}}^{(i)} \leftarrow \frac{\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B}}{\sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}}$$,
这里$\epsilon > 0$是一个很小的常数，保证分母大于0。在上面标准化的基础上，批量归一化层引入了两个可以学习的模型参数，拉伸（scale）参数 $\boldsymbol{\gamma} $和偏移（shift）参数 $\boldsymbol{\beta}$。这两个参数和$\boldsymbol{x}^{(i)}$形状相同，皆为$d$维向量。它们与$\boldsymbol{x}^{(i)}$分别做按元素乘法（符号$\odot$）和加法计算：

$${\boldsymbol{y}}^{(i)} \leftarrow \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}}^{(i)} + \boldsymbol{\beta}.$$

至此，我们得到了$\boldsymbol{x}^{(i)}$的批量归一化的输出$\boldsymbol{y}^{(i)}$。 值得注意的是，可学习的拉伸和偏移参数保留了不对$\hat{\boldsymbol{x}}^{(i)}$做批量归一化的可能：此时只需学出$\boldsymbol{\gamma} = \sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}$和$\boldsymbol{\beta} = \boldsymbol{\mu}_\mathcal{B}$。我们可以对此这样理解：如果批量归一化无益，理论上，学出的模型可以不使用批量归一化。
BN具体算法过程

如上图所示，BN步骤主要分为4步：

• 求每一个训练批次数据的均值
• 使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布。其中ε是为了避免除数为0时所使用的微小正数。
• 尺度变换和偏移：将xi乘以γ调整数值大小，再加上β增加偏移后得到yi，这里的γ是尺度因子，β是平移因子。这一步是BN的精髓，由于归一化后的xi基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数：γ,β。 γ和β是在训练时网络自己学习得到的。

对卷积层做批量归一化

对卷积层来说，批量归一化发生在卷积计算之后、应用激活函数之前。如果卷积计算输出多个通道，我们需要对这些通道的输出分别做批量归一化，且每个通道都拥有独立的拉伸和偏移参数，并均为标量。设小批量中有$m$个样本。在单个通道上，假设卷积计算输出的高和宽分别为$p$和$q$。我们需要对该通道中$m \times p \times q$个元素同时做批量归一化。对这些元素做标准化计算时，我们使用相同的均值和方差，即该通道中$m \times p \times q$个元素的均值和方差。

Pytorch 示例

BatchNorm1d

import torch
batchInput = torch.randn(4,3,784)
layer = torch.nn.BatchNorm1d(num_features=3,affine=True) #通道数
out = layer(batchInput)
print(batchInput.shape)
print(layer.running_mean)
print(layer.running_var)

输出

torch.Size([4, 3, 784])
tensor([0.0018, 0.0010, 0.0023])
tensor([1.0001, 0.9956, 0.9979])

BatchNorm2d

输入为4张3通道的彩色RGB图像，图像尺寸为28×28

batchInput2 = torch.randn(4,3,28,28)
layer2 = torch.nn.BatchNorm2d(num_features=3,affine=True) #通道数
out2 = layer2(batchInput2)
print(layer2.running_mean)
print(layer2.running_var)
print(vars(layer2))

权重参数和偏差参数分别为$\boldsymbol{W}$和$\boldsymbol{b}$：

print(layer2.weight)
print(layer2.bias)

output:

tensor([0.6736, 0.3242, 0.7500], requires_grad=True)
tensor([0., 0., 0.], requires_grad=True)

再看下归一化后的数据分布：全局均值与方差

print(layer2.running_mean)
print(layer2.running_var)

output:

tensor([-0.0009,  0.0008, -0.0017])
tensor([1.0034, 1.0035, 0.9970])

可以看出数据已经符合均值为0，方差为1的分布。