卷积网络输出尺寸

  • 输入图像大小$W*W$
  • 滤波器Filter大小$F*F$
  • 步长 $S$
  • padding的像素$p$

于是我们可以得出：
$N = (W − F + 2P )/S+1$

卷积神经网络如何工作

卷积网络不是一次只关注一个像素，而是接收方形的像素块并将它们传递给滤波器。该滤波器也是比图像本身小的方阵，滤波器的工作就是在像素中找到模式（特征提取）。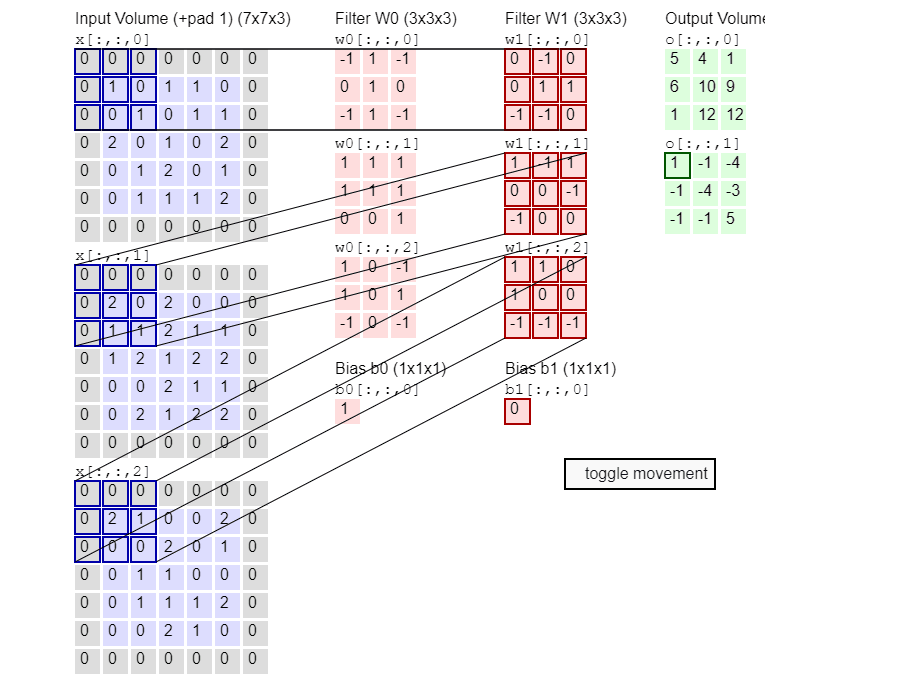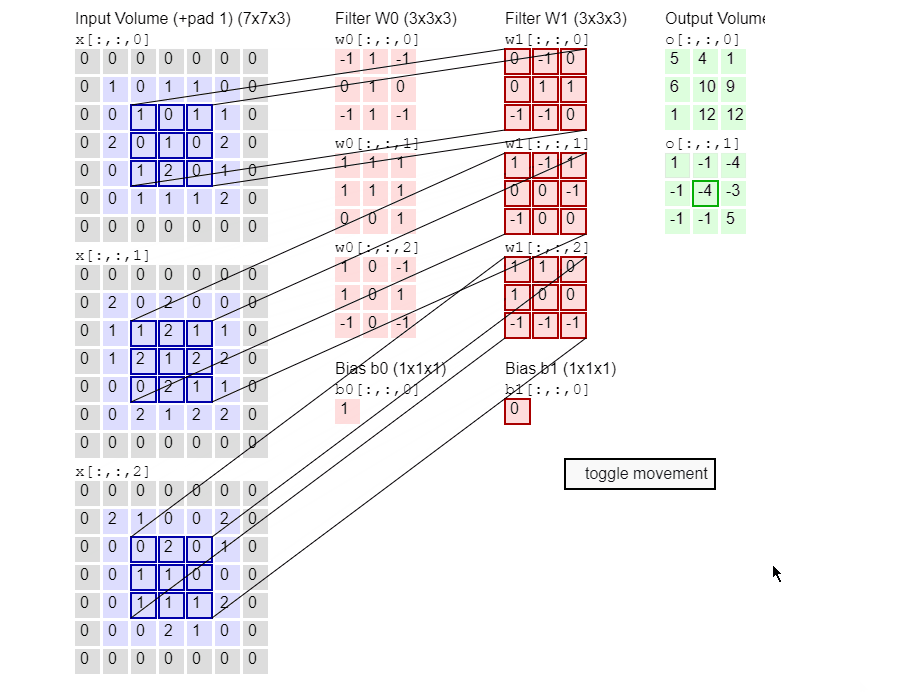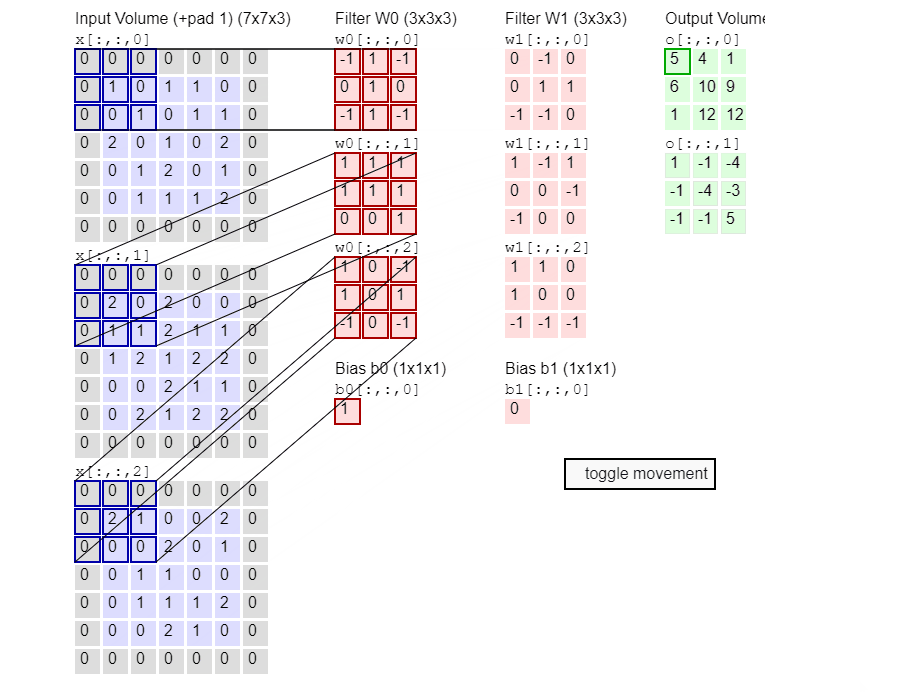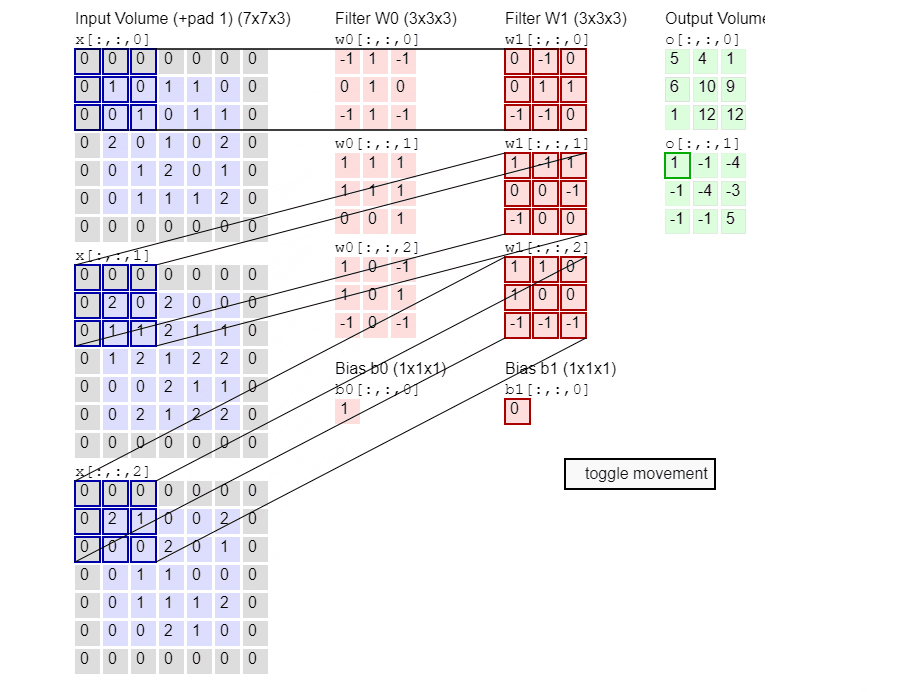
CV.gif-413.7kB

Multi-Kernels

$batch$张图片，每张图片是RGB三通道的彩色图，图像大小是5×5。

$$x:[batch,3,5,5]$$

如果是一个滤波器，滤波器大小为$3×3$，卷积核的厚度对应Feature Maps的通道数,即3。

$$one kernel:[3,3,3]$$

如果是一组滤波器（即多个滤波器），滤波器大小为$3×3$，卷积核的厚度对应Feature Maps的通道数,即3，共2组滤波器。

$$multi kernels:[2,3,3,3]$$

每个滤波器一个bias,则bias的size:
$$bias:2$$

则输出的size:

$$N = (W − F + 2P )/S+1 = (5-3+2)/2+1 =3$$

$$out:[batch,2,3,3]$$

LeNet-5

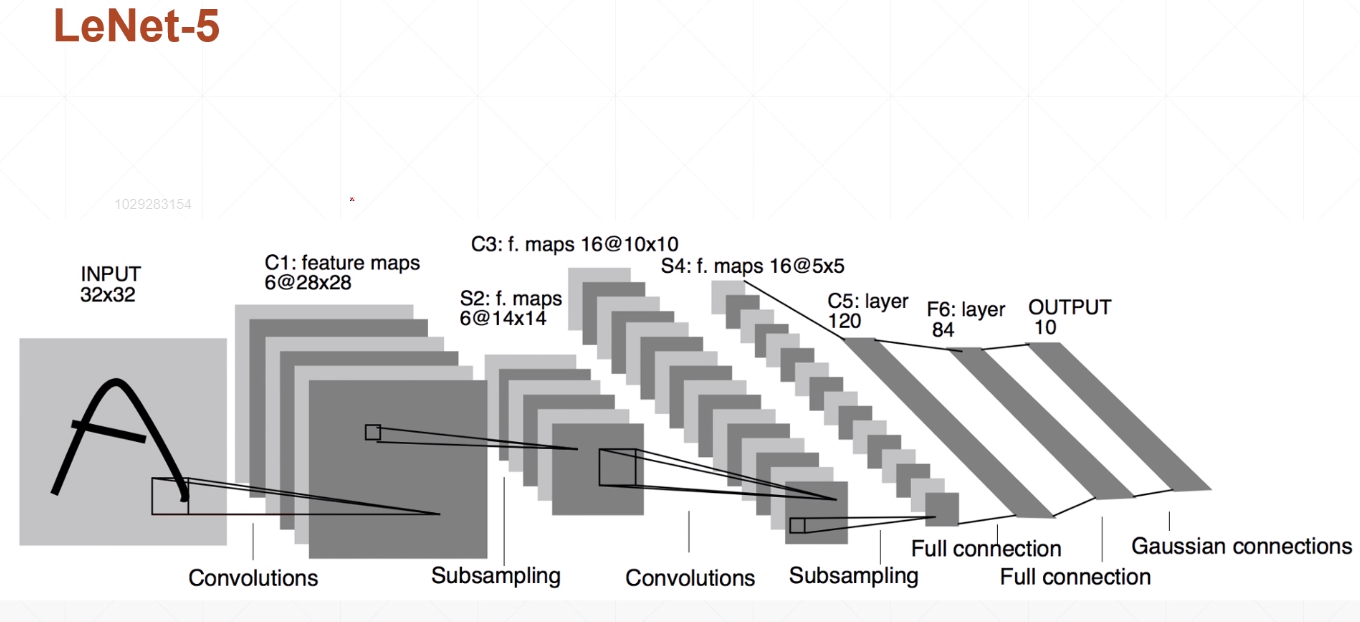
image_1dcgggjq3q2abujmqrc221obu15.png-319.5kB

INPUT层-输入层

  • 输入层图像的尺寸为$32×32$

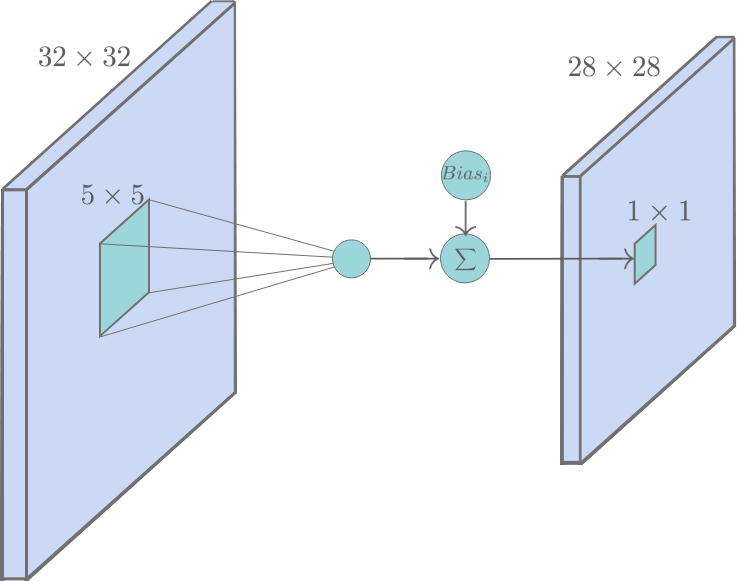
C1 卷积层

  • 输入图片：32*32
  • 卷积核大小：5*5
  • 卷积核种类：6
  • 输出featuremap大小：28×28 $（32-5+2×0)/1 + 1=28$
  • 神经元数量：28×28×6
  • 训练参数：$5×5×6+6=（5×5+1)×6 $

    每个滤波器5×5=25个unit参数和一个bias参数，一共6个滤波器

  • 连接数：（5×5+1）×6×28×28=122304

    C1内的每个像素都与输入图像中的5×5个像素和1个bias有连接，所以总共有156×28×28=122304个连接（connection）
    image_1dcgj3p7k17us30r1gck1rqp1afc2m.png-56.9kB

S2层-池化层（下采样层）

  • 输入：28*28
  • 采样区域：2*2
  • 采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
  • 采样种类：6
  • 输出featureMap大小：14×14（28/2）
  • 神经元数量：14×14×6
  • 可训练参数：2×6（和的权+偏置）
  • 连接数：（2×2+1）×6×14×14
  • S2中每个特征图的大小是C1中特征图大小的1/4
  • 详细说明：第一次卷积之后紧接着就是池化运算，使用 22核 进行池化，于是得到了S2，6个1414的 特征图（28/2=14）。S2这个pooling层是对C1中的2*2区域内的像素求和乘以一个权值系数再加上一个偏置，然后将这个结果再做一次映射。于是每个池化核有两个训练参数，所以共有2x6=12个训练参数，但是有5x14x14x6=5880个连接。

image_1dcgj3bdc6ni1gpvr791dulmbs29.png-65.2kB

C3层-卷积层

  • 输入：S2中所有6个或者几个特征map组合
  • 卷积核大小：5×5
  • 卷积核种类：16
  • 输出featureMap大小：10×10 (14-5+1)=10

C3层由16个10x10的特征图组成，与C1的最大区别是，这里每个特征图中的元素会与S2层中若干个特征图中处于相同位置的5x5的区域相连，如图所示：
image_1dcgj6nn417fk1comqal1u1omrn3j.png-13kB
而其具体的连接方案如下表所示：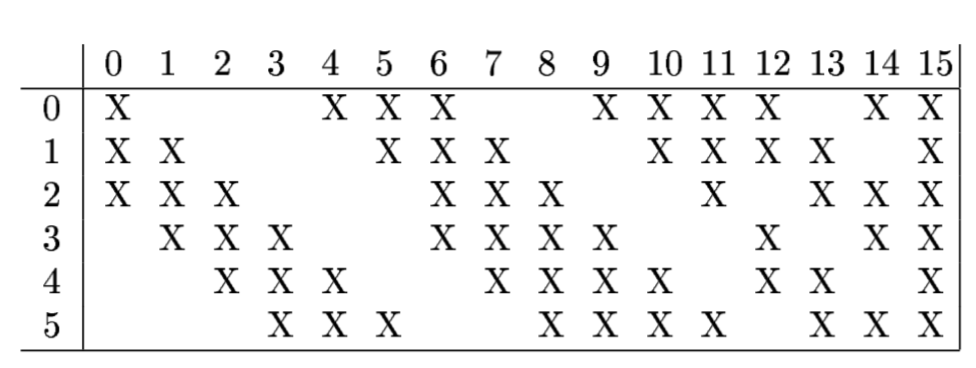
lenet_c3.png-90.1kB
具体来说，C3层中首先会将得到的对应的卷积结果相加，然后再进行类似C1层的加偏置的操作，从而得到一个元素。按照上表中的规则连接，C3层一共有$6 \times (3 \times 25 + 1) + 9 \times (4 \times 25 + 1) + 1 \times (6 \times 25 + 1) = 1,516$个可训练的参数，一共有$151,600$个连接。

另外，值得说的一点是，为什么要采用上面的连接方案，而不是“全”连接？首先，不完全的连接可以减少参数和连接数；其次，我们知道每个特征图对应的就是卷积核从输入中提取出的不同的特征(特征提取)，采取这种不对称的连接，可以使本层的特征图对应的不同的更高级的特征。

S4层(池化层)

  • 采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
  • 滤波器种类：16
  • 可训练参数：2*16=32
    S4层是一个池化层，他由16个5x5的特征图构成，其操作和S2层相同。其共有32和可训练的参数和2000个连接。

###C5层(卷积层)
输入：S4层的全部16个单元特征map（与s4全相连）

  • 卷积核大小：5*5
  • 卷积核种类：120
  • 输出featureMap大小：1*1（5-5+1）
  • 可训练参数/连接：120（165*5+1）=48120

    C5是一个类似C3的卷积层，由120个1x1的特征图组成。但是，与C3层不同的是，这里的连接是一种“全”连接，即每个特征图中的元素与S4层中每个特征图都连接。
    一共有120×(5×5×16+1)=48120个可训练的参数。

F6层(全连接层)

F6就是一个简单的全连接层，它由84个神经元构成。和传统的全连接一样每个神经元将C5层中的特征图的值乘上相应的权重并相加，再加上对应的偏置再经过tanh激活函数。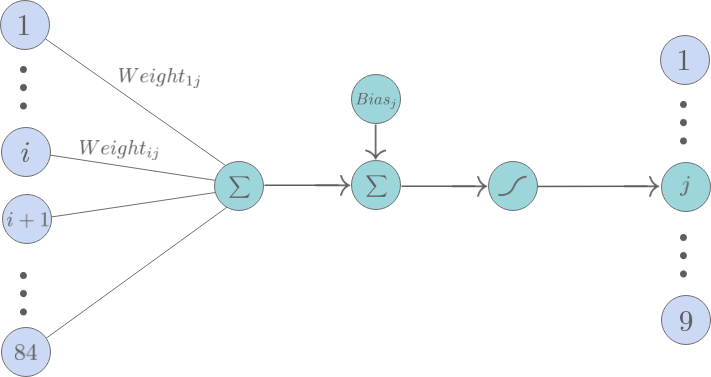
image_1dcgk9umqjse40udm71tvgvku7p.png-43.4kB
F6层共有84×(120+1)=10,164个可训练的参数。

输出层

输出层由10个欧几里得径向基函数核(Euclidean Radial Basis Function, RBF)构成，每个核对应0-9中的一个类别。输出值最小的那个核对应的i就是这个模型识别出来的数字。

  • RBF核的输出

$$y_i = \sum_j{(x_j - w_{ij})^2}.$$

其中，$ x_i \in \vec{X} = { x_1, … , x_i, … x_{84} } $，$\vec{X}$ 就是F6层中的神经元的输出组成的向量。 而$w_{ij} \in \vec{w_i} = { w_{i1}, … , w_{ij}, … x_{i84} }$，是数字i对应的RBF核保有的一个常向量。 即，RBF核的输出就是输入向量$\vec{X}$ 和$\vec{w_i}$的欧几里得距离。

RBF核保有的常向量wi→中的元素是+1或者-1，这些向量被人为设定为可以表示绘制在7x12位图上的字符(0—9)，这也就解释了为什么要将F6层设定为84个神经元。至于为什么要这么设计？主要是为了保证该模型在被拓展应用到识别ASCII码时，该模型可以正确区别例如0和大小写O，这种容易混淆的字符。
下图是RBF核保有的常向量对应的bitmap字符：

image_1dcgkndup1p1r1a581rb7188lv6386.png-117.3kB