什么是卷积

在泛函分析中，卷积（convolution)是一种函数的定义。它是通过两个函数$f(x)$和$g(x)$生成第三个函数的一种数学算子，表征函数$f(x)$和$g(x)$经过翻转和平移的重叠部分的面积。

卷积的数学定义

  • 离散型

    其中星号表示卷积。当时序x=0时，序列$g(-t)$是$g(t)$的时序$t$取反的结果；时序取反使得$g(t)$以纵轴为中心翻转180度，所以这种相乘后求和的计算法称为卷积和，简称卷积。另外，x是使$g(-t)$*位移的量**，不同的$x$对应不同的卷积结果。深度学习卷积神经网络中的卷积就是这种类型，两个变量在某范围内相乘后求和的结果。
    $$y(x)=f(x) * h(x) =\sum_{t=-\infty}^{\infty} f(t) g(x-t)$$

  • 连续型

    其中$t$是积分变量，积分也是求和(离散型)，x是使函数g(-t)位移的量，星号$$表示卷积。
    $$h(x)=f(x)    g(x)=\int_{-\infty}^{+\infty} f(t) g(x-t) \mathrm{d} t$$

那么我们看到这个积分公式里面$f(t)$、$g(t)$是什么呢？其实是这样，$f(t)$不动，$g(t)$相当于函数$g(t)$沿着$y$轴$(t=0)$做了一次翻转。$g(x-t)$表示$g(-t)$的沿着$t$轴向右便宜了$+x$个单位。
明白这个变换后可知，这是两个函数，一个固定函数$f(t)$，一个是滑动函数$g(t)$,求他们相乘之后围起来的面积。

图解卷积

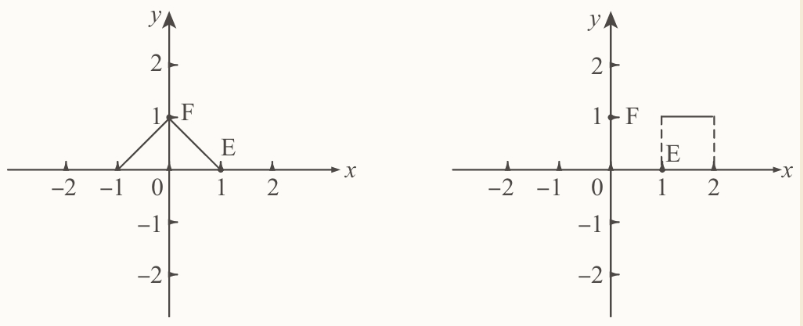
5.png-23.2kB
$f(t)$就是一个三角，在第二象限是一条过$（-1，0）$和$（0，1）$点的线段，在第一象限是一条过（0，1）和（1，0）点的线段。
函数$g(t)$是一个正方的脉冲波，t在[1，2]上有定义，在这段区间里$g(t)=t$。函数$g(x-t)$是左侧的这个做过翻转的图形，图示中还分别有$x=-2$，$x=-1$，$x=0$，$x=1$，$x=2$时的图像。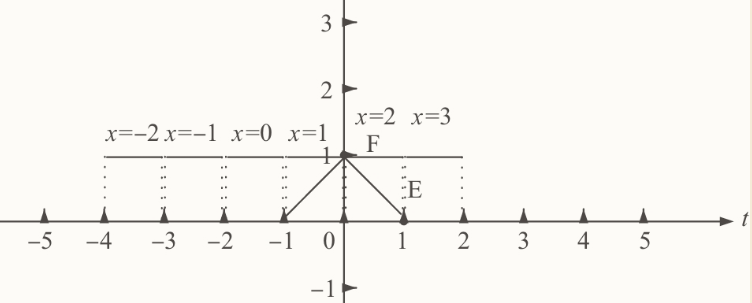
11.png-26.6kB
我们观察到，在这个不定积分完毕后，会形成两个函数叠加的部分，其中$x$是一个变量。假设$x$为0，或者我们当$x$压根不存在，那么就是$f(t)$和$g(-t)$这两个函数相乘后和$y=0$（t轴）围成的面积。当x出现后，x是帮着$g(x-t)$图像左右平移的，刚刚我们也看到这个图像的变化过程了，那么会变成什么样？简单说，这个函数$h(x)$的值就是求一个面积和$x$的关系，而这个所说的面积就是函数$f(t)$与$g(x-t)$卷积后的曲线和y=0（t轴）围成的面积，其中自变量是$x$。在随着x变化的移动过程中，由于$g(x-t)$移动产生的$h(x)$的对应变化就是整个卷积公式的意义了——一个移动中用$x$进行取样的过程，或者说特征提取。

卷积核

当我们能够理解卷积的含义之后，那理解卷积核就会简单多了，因为我们只要理解它是在滑动中去提取特征就足够了。
我们先看卷积核的表达方式，它的表达式为
$$f（x）=wx+b$$
可能有人会问是不是写错了，这不是卷积核，这就是一个普通的神经元的线性处理的部分。其实你这么看倒是也不能算错，因为从计算逻辑的角度来看还真差不多。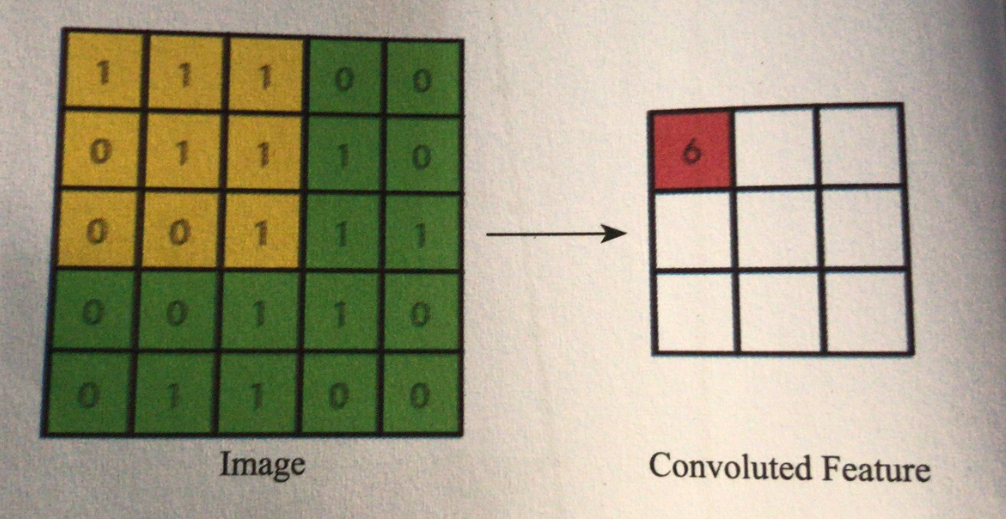
5555.png-1387.1kB
我们先想象这里有一张图片，图片有5×5一共25个像素点，每个像素点只有1和0两种取值。那么提取这样的一种图的特征，我们可以先随便设计一个卷积核来看看到底会产生什么结果，我们设计一个特别简单的卷积核。
$$w=[1，1，1，1，1，1，1，1，1]，b=[0]$$
$w$由9个1构成，在这个场景里，我们指图中黄色部分的这个$3×3$的小方框，从左到右从上到下的这9个点作为$x$向量，挨个与$wv相乘完成内积操作，并与$b$相加。这个过程就是这样了：
$$f(x)=1×1+1×1+1×1+1×0+1×1+1×1+1×0+1×0+1×1+0=6$$

那么左上角的这个黄色小方框就会输出一个6，我们把6单独存在一个存储空间里，这个存储空间就叫做这个卷积层的Feature Map，也就是图中所示的Convoluted-Feature这个部分。我们看在这样一个操作下，9个点的信息被压缩成了一个点，当然这肯定是有损压缩了，还原肯定是还原不回去了(卷积不可逆)。不过确实在这个过程中有这样一个信息抽象的过程，大家请注意，这个抽象过程就是特征提取。

我们把这个小黄方框的操作继续从左到右，从上到下每次移动一个方格，就相当于前面我们说的$f(t)和$g(x-t)两个函数通过$x$变化来滑动一样做这样一个卷积操作，那么右侧的Feature-Map的每个点的值也都能对应产生结果了。根据我们设计的卷积核的$w$和$b$的值，剩下的8个输出值应该分别是：7、6、4、7、7、4、6、6。这样一来25个点的信息量就被压缩成了9个点，完成了特征提取和压缩两个功能。

在卷积核的$f(x)=wx+b$输出后还可能会跟着一个激励函数而且也一般会定义一个激励函数跟随其后，现在的CNN网络中的激励函数非常喜欢用ReLU。不过你也会发现在实际工作中，可能会用别的激励函数跟在卷积核后面进行工作，或者不用激励函数。理由通常都是为了在一些特殊的场景中有更好的表现，共性我还没总结出来，不过ReLU作为激励函数的场合应该说是最常见的。
卷积核中的$w$、$b$需要通过训练来得到，是模型中非常重要的参数。

卷积层的其他参数

在卷积核对上一层输入的向量进行扫描的时候，还有几个别的参数需要注意，一个是Padding（填充），一个是Striding（步幅）。
先说Padding，Padding是指用多少个像素单位来填充输入图像（向量）的边界。就像图上所画，在这四周的区域里都进行Padding，通常都是填充0值。当然一般不会有像我们图上画的这么大比例的Padding了，在800×600的图过卷积层的时候，能在四周各Padding上5到10个单位就不少了。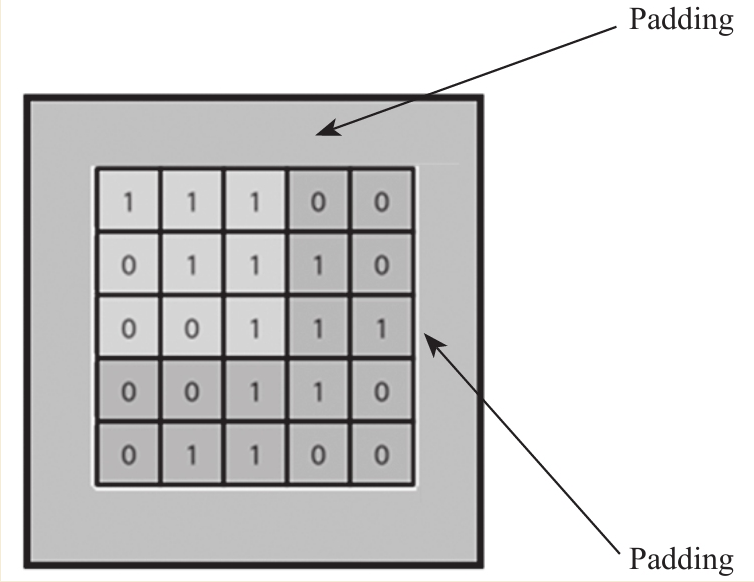
555.png-132kB
Padding的用途大概可以理解为两种目的。

  • 目的1： 保持边界信息。因为如果不加Padding的话，最边缘的像素点信息其实仅仅被卷积核扫描了一遍，而图像中间的像素点信息会被扫描多遍，在一定程度上等于降低了边界上信息的参考程度。Padding后就可以在一定程度上解决这个问题。在实际处理的过程中肯定是Padding了一些0值以后，再从Padding后的新边界开始扫描。
    • 目的2： 如果输入的图片尺寸有差异，可以通过Padding来进行补齐，使得输入的尺寸一致，以免频繁调整卷积核和其他层的工作模式。

Stride就是步幅，在卷积层工作的时候，Stride可以理解为每次滑动的单位。比如刚刚这个例子，我们用的就是Stride=1的情况——每次只滑动一个单位。在实际工作中Stride=1的使用场景很多，因为它对于采用的细密程度保证得最好。当然Stride也可以取别的值，比如Stride=3，那么扫描的时候就不是每次移动1个像素，而是每次移动3个像素了。这种方式直观上想一想就会觉得比较“粗糙”，因为跳过的像素行列的信息明显扫描的次数降低了。不过好处也显而易见，就是因为处理的次数变少了，所以卷积层在扫描的时候工作会变快，这可能是唯一的好处。在设计网络的时候，Stride取多少合适需要经过测试，先设置Stride=1，如果工作状况已经很理想了，而希望通过加大Stride来获得一些性能的提升或者存储量的减小，那么可以逐步尝试调整为Stride=2或其他值。一切都以实测结果为准，到目前为止这个值究竟应该设定为多少还没有一个确切的有效的判断方法。

池化层

池化层（Pooling Layer，或称池层）是在一些CNN网络中喜欢设计的一层处理层。池化层的作用实际上对Feature Map所做的数据处理又进行了一次所谓的池化处理。我们具体来看看这个池化处理都做了些什么吧。
常见的池化层处理有两种方式：一种叫Max Pooing，一种叫Mean Pooling（也叫Average Pooling），顾名思义，一个做了最大化，一个做了平均化。除此之外还有Chunk-Max Pooling、Stochastic Pooling等其他一些池化手段。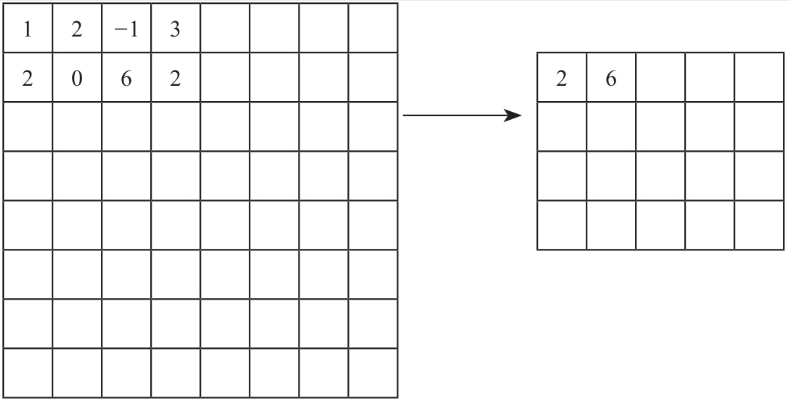
55.png-26.1kB
Max Pooling就是在前面输出过来的数据上做一个取最大值的处理，比如以Stride=2的2×2为Max Pooling Filter（滤波器，我们就理解为跟卷积类似的特征处理就好了）之后，左上角就出现了这样的变化。临近的4个点取一个最大值成为Max Pooling层中的储存值。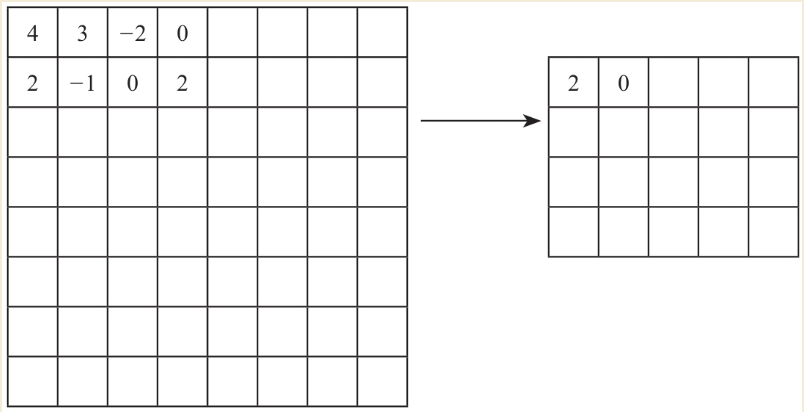
111.png-27.6kB
Mean Pooling就是在前面输出过来的数据上做一个取平均值的处理，比如以Stride=2的2×2为Mean Pooling Filter之后，左上角就出现了这样的变化。临近的4个点取平均值输出到Mean Pooling中保存起来，如图所示。

一般来说，池化层被认为有这样几个功能。

  • 它又进行了一次特征提取，所以肯定是能够减小下一层数据的处理量的。
  • 由于这个特征的提取，能够有更大的可能性进一步获取更为抽象的信息，从而防止过拟合，或者说提高一定的泛化性。
  • 由于这种抽象性，所以能够对输入的微小变化产生更大的容忍，也就是保持其不变性。这里的容忍包括图形的少量平移、旋转以及缩放等变化。
    池化层在CNN网络中不是一个必需的组件，一些新的CNN网络在设计的时候也没有池化层出现。